1. Vector intro for linear algebra
Vector has both magnitude and direction.
- Speed is not a vector. This is considered to be a scalar quantity. If we want it to be a vector, we would also have to specify the direction.
- Velocity is a vector because it has magnitude and direction.
And the interesting thing is that we only care about magnitude & dirrection. We don't necessarily not care where we start and where we place.
2. Real coordinate spaces
When you see R2 in your textbook, it means that 2-dimensional real coordinate space.
- 2 tells how many dimensions are there.
- R tells Real Cartesian coordinate space. This space is all the possible real-valued 2-tuples.
- tuple means an ordered list of numbers. neither numbers have imaginary numbers.
3. Adding vectors
They are the some regardless of Addition order
4. Multiplying a vector by a scalar
- If you multiply -1, then the direnction of vector will be exactly opposite!
- If you multiply possitive number scalar except 1, then the magnitude of vector will be changed!
- ex. multiplying with a negative scalar
a = [2,1]
-1a = [-2, -1]
5. Vector examples
Standard position is just to start the vectors at 0, 0 and then draw them.
You can start vector at any point in R2
- Subtraction
ex. x = [2,3], y = [-4, -2]
x - y = x + (-1 * y) = [6, 5]
y - x = [-6 ,-5]

- Generalization (not only in 2-D space)
ex. In R4
a = [0, -1, 2, 3] , b = [4, -2, 0, 5]
4a - 2b = [-8, 0, 8, 2]

6. Unit vectors intro
Unit vector is a vector which has length 1.
Any 2-dimensional vectors can be represented with two vectors(i=[1,0], j=[0,1])

v = 2i + 3j
7. Parametric representations of lines
Let's define some vectors.
Ex1
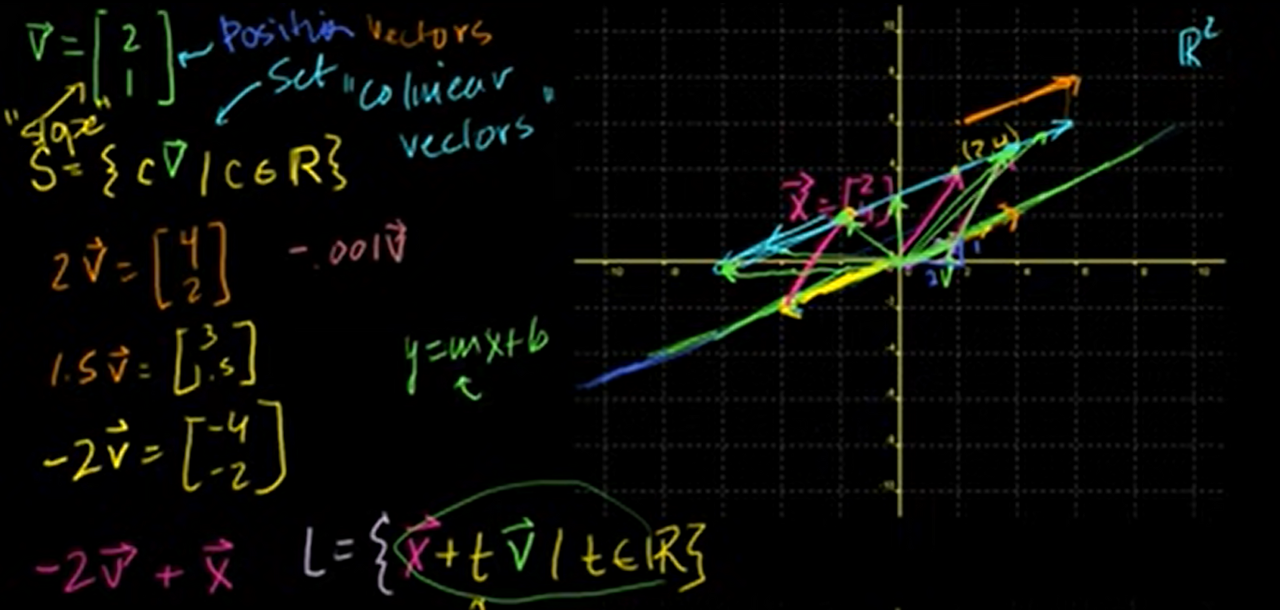
starts at the origin because is a position vector.
S =
What if we want to represent a parallel line that goes through that point over (2,4)?
And let's define another set.
L =
- t is parametrization of the line
Why should we use L instead of y=mx+b equation?
y=mx+b can only work well in R2. But line L can work at any dimension. That's why we represent a line like that.
Ex2
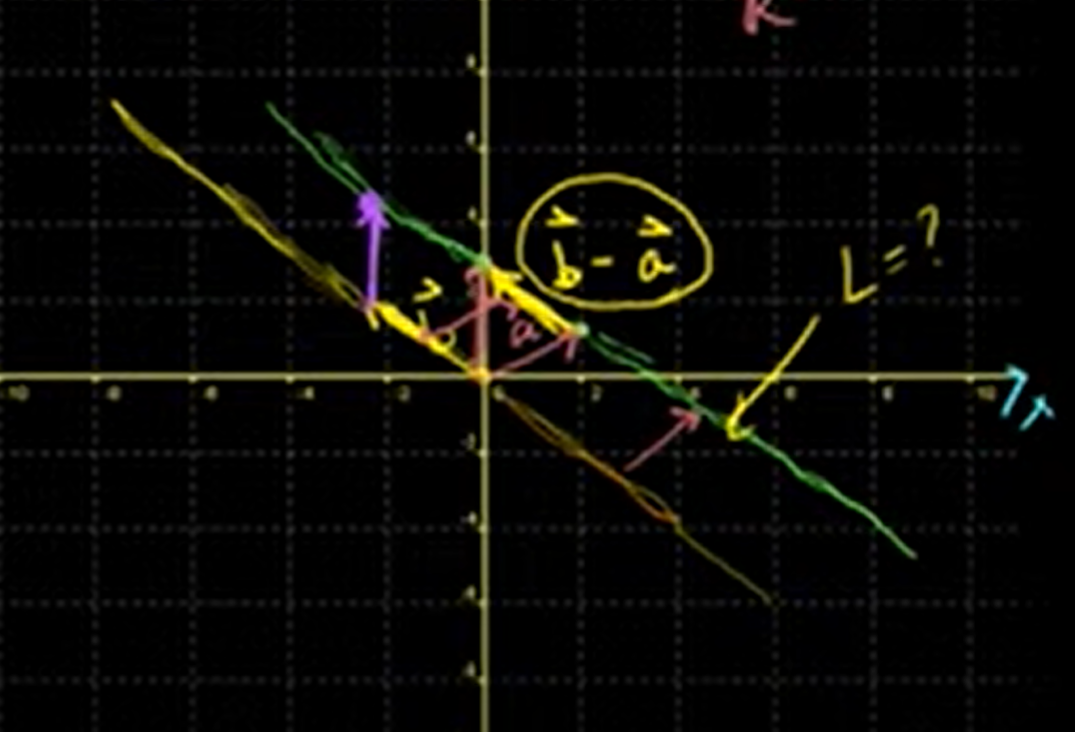
,
L =
We can also represent like this way.
Li = [L1, L2] =
- L1: x-coordinate
- L2: y-coordinate
It's really easy in 2-Dimensional space, but how do you present lines in three dimensions?
Ex3
,
These vectors are in R3.
L =
- x-coordinate = -1 + (-1)t
- y-coordinate = 2 + (-1)t
- z-coordinate = 7 + 3t
Then our line can be described as a set of vectors.
As we are dealing in R3, the only way to define a line is to have a parametric equation.
x+y+z = k is not a line!! This is a plane. The only way to define a line or a curve in three dimensions, it has to be a parametric equation!.
'Computer Science > Linear Algebra' 카테고리의 다른 글
| 06 Matrices for solving systems (0) | 2022.02.24 |
|---|---|
| 05. Vector dot and cross products (0) | 2022.02.22 |
| 04. Subspaces and the basis for a subspace (0) | 2022.02.22 |
| 03. Linear dependence and independence (0) | 2022.02.22 |
| 02. Linear combinations and span (0) | 2022.02.22 |



